Estatísticas Probabilísticas

Variáveis aleatórias discretas: sem valores decimais, são valores inteiros. Exemplo: quantidade de filhos.

Variáveis aleatórias continua: qualquer valor contidos nos números reais. Exemplo: salário, distância entre cidades.

Variáveis discretas

Distribuição de probabilidade:

• Uniforme
• Bernoulli
• Binomial
• Binomial negativa
• Poisson

Distribuição uniforme discreta: Todos os valores possíveis têm a mesma probabilidade de ocorrência. Exemplo: As probabilidades dos resultados possíveis ao lançar 1 DADO são: 1,2,3,4,5 ou 6. A probabilidade de tirar 1 desses números pode ser modelada pela distribuição uniforme discreta, pela formula ficaria: p(Xi) = 1/n ==> p(x=1)=1/6 , p(x=2)=1/6,… sempre 1/6 é a probabilidade de tirar 1 desses números no DADO.

Distribuição de Bernoulli (Logística binária): os valores da variáveis podem assumir apenas 2 resultados, sendo sucesso (x=1) ou fracasso (x=0), ou Sim (x=1) e Não (x=0). Formula: ( P(X = x) = p^x (1 – p)^{1 – x} ), onde ( x ) pode ser 0 ou 1.

Distribuição binomial (Logística multinomial): A variável do modelo binominal indica a quantidade de sucesso (k) nas (n) repetições. Onde você tem 3 ou mais resultados. Formula: P(X = x) = (n x) p^x (1 – p)^(n-x).

Distribuição binomial negativa: A probabilidade de sucesso(p) é constante em todos os ensaios realizados. A variável no modelo binomial negativa indica a quantidade de ensaios (x). A diferença entre a binomial, é que na binomial você tem a quantidade de repetições e você analisa quantos sucessos ocorrem nessas n repetições, já na binomial negativa você analise quantos ensaios são necessários para atingir aquele sucesso estabelecidos.

Fonte: https://www.ime.usp.br/~kevinx/SAEB/help/PBinomialNegativa.html. Acesso: 30 outubro 2024.

Distribuição poisson: A probabilidade de ter (k) sucessos, mas agora você deve definir a exposição contínua.

Exemplo exposição contínua: tempo e área.

Variáveis contínuas

Distribuição de probabilidade:

• Normal
• Qui-quadrado
• t de Student
• F de Snedecor

Distribuição normal: Gaussiana, com curva em formato de sino. Baseada na média e do desvio padrão da variável. É simétrica em torno da média. Quanto menor o desvio padrão, mais concentrados estão os valores em torno da média.

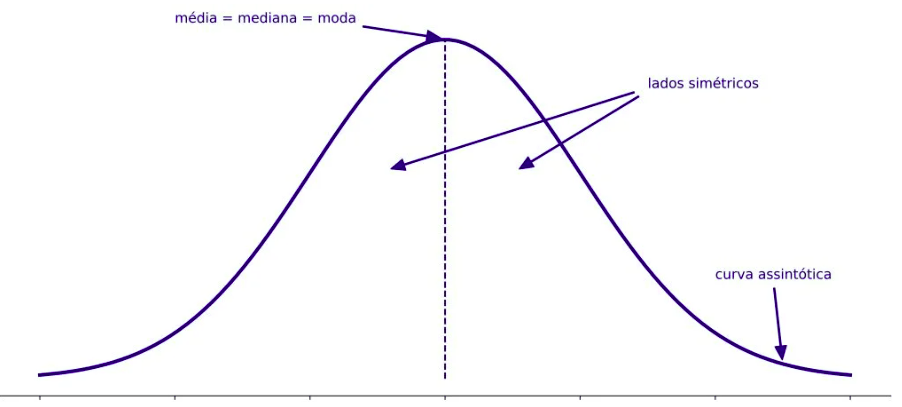
Fonte: https://www.blog.psicometriaonline.com.br/distribuicao-normal/, acessado 31 outubro 2024.

No centro temos a média. Ou seja, são simétricas em torno da média, ou seja, metade das probabilidades estão acima da média e a outra metade abaixo da média.

z-score, para transformar em uma distribuição normal padrão. indica a distância de um valor em relação à média de um conjunto de dados, calculando os dados em uma distribuição com média 0 e desvio padrão 1.

São utilizados em diversas áreas, ele descreve a relação entre um valor e a média de um grupo de valores. Podem ser tanto negativos, quanto positivos os Z-Scores. O valor positivo mostra que a pontuação está acima da média e a pontuação negativa mostra que está abaixo dessa média. Em finanças, por exemplo podem ser utilizados como medidas de variabilidade de uma observação e ajudar traders a determinar a volatilidade do mercado.

Com o z-score conseguimos achar as area do grafico, que são as Zs:

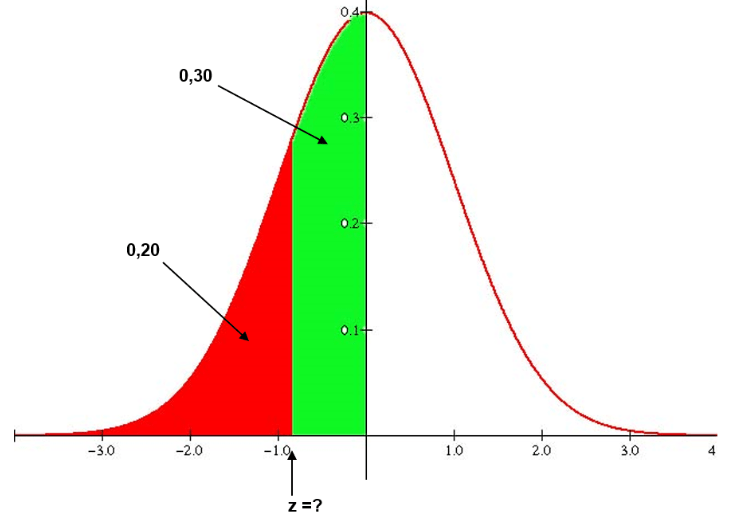
Fonte: https://professorguru.com.br/estatistica/distribuicao-normal.html, acesso 04 novembro 2024.

Exemplo de exercícios que conseguimos achar nas áreas Z:

“O salário semanal dos operários de construção civil de certo país é distribuído normalmente em torno da média de $ 80, com desvio padrão de $5.

a) Qual é o valor do salário para escolhermos 10% dos operários com maiores remunerações?

b) Qual é o maior salário correspondente aos 20% dos trabalhadores que ganham menos?”

Distribuição qui-quadrado: Diferente da distribuição normal, a qui-quadrado depende de 1 parâmetro chamado de grau de liberdade.

A distribuição tem curva assimétrica e positiva para valores mais baixos nos graus de liberdade. Utilizado em testes de associação entre variáveis categóricas. Exemplo: Achar valores críticos e probabilidades associadas á distribuição qui-quadrado.

Gráfico assimétrica positiva é com cauda alongada para direita:

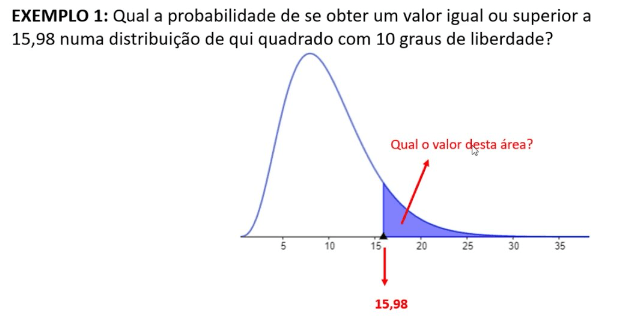
Fonte: https://www.youtube.com/watch?v=th1bdIuExkg, acesso: 04 novembro 2024

Distribuição t-studente: Parece muito com a normal padrão, forma de sino e é simétrica em torno da média.Porem a t-student tem a cauda mais alongada, ou seja, permite visualizar valores mais nos extremos e dependem do grau de liberdade.

Fonte: https://pt.wikipedia.org/wiki/Teste_t_de_Student, acesso 4 novembro 2024.

Distribuição F de Snedecor (distribuição de Fischer): Muito utilizado para analise de variância. Forma assimétrica e positiva quando os graus de liberdades são pequenos. São 2 parâmetros graus de liberdade no numerador e grau de liberdade no denominador, a forma da curva depende do grau de liberdade.