“Em testes de hipóteses estatísticas, diz-se que há significância estatística ou que o resultado é estatisticamente significante quando o p-valor observado é menor que o nível de significância α. α definido para o estudo“. Fonte: https://pt.wikipedia.org/wiki/Signific%C3%A2ncia_estat%C3%ADstica

“Por exemplo, a hipótese nula é rejeitada a 5% quando o p-valor é menor que 5%“. Fonte: https://pt.wikipedia.org/wiki/Signific%C3%A2ncia_estat%C3%ADstica

Correlação mosta Direção e Força e Teste de Hipótese mostra a Confiança.

Finalidade:

• Verificar a variância, o quanto varia em relação a média e o desvio padrão
• Dependendo do tamanho da base de dados/população, utilizamos a amostra para analise.
• Para testar o parâmetro de interesse da amostra, utilizamos os teste de hipótese estatísticas.

Resumo:

1. Hipótese Nula (H₀): Afirma que não há efeito ou diferença.
2. Hipótese Alternativa (H₁): Afirma que há um efeito ou diferença significativa.
3. Nível de Significância (α): Limite para rejeitar H₀, geralmente 0,05 (5%).
4. Valor-p (p-value): Probabilidade de obter os resultados observados (ou mais extremos), assumindo que H₀ seja verdadeira.

• Se p ≤ α: Rejeita-se a hipótese nula; os resultados são considerados estatisticamente significantes.
• Se p > α: Não há evidências suficientes para rejeitar H₀.

Testes de hipóteses tradicionais:

• Teste t de Student: Compara as médias de dois grupos.(amostra menores)
• ANOVA (Análise de Variância): Verifica diferenças entre três ou mais grupos.
• Qui-quadrado (χ²): Avalia associações entre variáveis categóricas.
• Teste de Wilcoxon e Mann-Whitney: Testes não paramétricos para comparar medianas entre grupos.

Alguns Exemplo de Uso:

1. Modelos de regressão:
   • Nos modelos de regressão (linear, logística, etc.), a significância é usada para avaliar se os coeficientes das variáveis independentes são estatisticamente diferentes de zero. Isso ajuda a determinar se essas variáveis têm uma relação significativa com a variável dependente.
2. Modelos de correlação:
   • Em análises de correlação (como o coeficiente de Pearson ou Spearman), a significância indica se a associação entre duas variáveis é relevante ou pode ser fruto do acaso.
3. Testes em machine learning:
   • Em técnicas como testes de permutação ou validações cruzadas, a significância estatística é usada para avaliar a performance de modelos em comparação a uma distribuição aleatória.

Explicação mais detalhada:

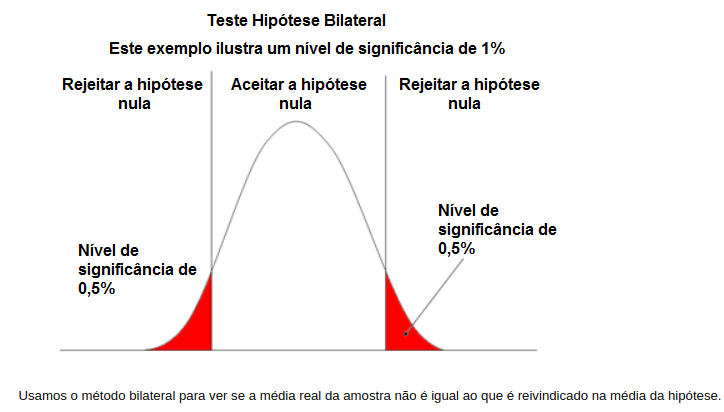
Teste bilateral (bicaudal): teste bilateral, o interesse é testar.

• Hipótese Nula (H0):  declara que não há relação entre dois fenômenos de interesse. Não ao efeito.
• Hipótese alternativa (H1): é estatisticamente diferente de certo valor de interesse. Afirmação e evidencia, podemos tratá-la como uma “novidade” ou “nova”. Ou seja, é a situação em que há algo de diferente.
• Sendo necessário ter definido o nível de significância (α) desejado para a análise.
• Estatisticamente diferente. (Hipótese alternativa. H1)

Os testes unilaterais você especifica a direção do teste, ou a esquerda ou a direita:

Teste unilateral (unicaudal), à esquerda:

• H0 – Hipoteste Nula
• H1 – Hipotese alternativa
• O objetivo é analisar se o parâmetro é estatisticamente menor do que certo valor de interesse. (Hipótese alternativa. H1)

Teste unilateral (unicaudal), à direita:

• Nesse teste unilateral à direita, para um parametro, o interesse é testar:
  • H0 – Hipoteste Nula
  • H1 – Hipotese alternativa
• Objetivo é verificar se o parâmetro é estatisticamente maior do que certo valor de interesse.(Hipótese alternativa. H1)

Fonte: https://pt.slideshare.net/JoaoAlessandro/aula-30-testes-de-hipteses-17921069#7 , acesso 05 novembro de 2024.

Fonte: https://www.learningaboutelectronics.com/Artigos/Calculadora-teste-de-hipotese-estatistica.php#google_vignette, acesso em 05 novembro de 2024.

Significância do teste

Indica a probabilidade de rejeitar H0 quando ela é verdadeira, ou seja, a probabilidade de cometer o erro tipo I:

Fonte: https://rpubs.com/mcouto/557755, acesso 05 novembro de 2024.

• Alguns níveis de significância utilizados:
  • α = 1% (ou seja, o nível de confiança do seu teste é de 99% = 1- α)
  • α = 5% (ou seja, o nível de confiança do seu teste é de 95% = 1- α)
  • α = 10% (ou seja, o nível de confiança do seu teste é de 90% = 1- α)
• Ou seja, o nível de confiança do teste é definido como 1 – α

P-valor e teste de hipótese

p-valor e nível de significância:

t critico, verificar qual o valor, que a direita é região critica, ou seja, região com 5%. RC região critica é a região de rejeição H0.

Quando o p-valor < α: Rejeita H0.

Quando o p-valor > α: Não Rejeita H0.

Teste Z para médias de uma amostra:

Quando utilizar teste Z:

• Quando eu conheço o desvio padrão populacional (banco de dados) .
• Quando a variável tem a aderência a normal.
• Ou quando estou utilizando para grandes amostras.
• Distribuição relevante para os valores críticos é a normal padrão.

Teste t para médias de uma amostra:

• Para amostras, bem parecido com teste Z, porem normalmente aplico o teste t quando não conhece o desvio padrão populacional , então utilizo o desvio padrão amostral.
• Distribuição t é usado com n-1 grau de liberdade.

Teste t para correlações:

• Após estimado o coeficiente de correlação (r) entre variáveis quantitativas, é possível testar a significância do parâmetro estimado.
• Distribuição relevante é a t de student com n-2 graus de liberdade.

Exemplo, imagina que encontrei a correlação, o coeficiente de correlação entre 2 variáveis quantitativas e agora quero ver se esse coeficiente de correlação é estatisticamente significante. Exemplo abaixo utilizado correlação de pearson, veja:

Com nível de significância de 5%, o exemplo acima é bicaudal será 2,5% para a esquerda do gráfico e 2,5% a direita do gráfico, o calculo do valor crítico revelou ser 2,048 (com n-2 grau de liberdade):

conclusão, o coeficiente de correlação “matemática-física” é estatisticamente diferente de 0 e é estatisticamente significante.

Teste qui-quadrado para uma amostra:

Aplicado quando tenho 1 variável categóricas onde ela pode assumir 2 ou mais categorias (k), objetivo é verificar se há diferenças entre as frequências observadas e esperada.

Exemplo de aplicação: Uma loja verificar se vende mais dependendo do dia da semana. Se acaso forem estatisticamente significante 5%, ou seja, no lado Não Critico do gráfico, não há evidencias que dependendo do dia da semana influencie na quantidade das vendas.

Teste F para comparação de variâncias:

• Para comparar as variâncias de duas amostras independentes.
• Distribuição relevante é a F de Snedecor, com n-1 graus de liberdade no numerados e n-1 graus de liberdade no denominador.

Intervalo de confiança

Intervalo de confiança para a média:

• Quando obtemos a estimativa para a média populacional a partir de uma amostra, tambèm podemos construir seu intervalo de confiança, isto é, um intervalo de valores possíveis para o parâmetro populacional.
• É necessario estabelecer o nível de confiança da análise (exemplo 95%)
• Z e t são valores bicaudais, na distribuição t utiliza-se n-1 graus de liberdade.

Exemplo: Imagine tendo a média amostral, mas você queira ter uma faixa de valores para conter os valores populacionais, a partir da sua média amostral. Pode usar a Z ou a T, a Z para grandes amostras conhecendo a média populacional, e a t para pequenas amostras e não conhecendo a média e desvio padrão.

Resumos Geral: (mais utilizados)

🔹 Testes Paramétricos (quantitativos e devem ter normalidade)

Teste t de Student (uma média, duas médias independentes ou emparelhadas)

ANOVA (Análise de Variância) e suas extensões (para comparar três ou mais médias)

Testes de normalidade: Kolmogorov-Smirnov, Shapiro-Wilk (amostra pequena), Shapiro-Francia

Testes de homogeneidade de variâncias: Bartlett, Cochran, Hartley, Levene


🔹 Testes Não Paramétricos (qualitativos ou ocorre violação de suposições paramétricas)

Qui-quadrado (χ²): para variáveis nominais ou ordinais, em uma ou mais amostras

Teste Binomial: para variáveis binárias (sucesso/fracasso)

Teste dos Sinais: para dados ordinais, em uma ou duas amostras emparelhadas

Teste de Wilcoxon: comparação de duas amostras emparelhadas

Mann-Whitney U: comparação de duas amostras independentes ordinais

Teste de McNemar: variáveis binárias emparelhadas

Friedman: k amostras emparelhadas (ordinais)

Kruskal-Wallis: k amostras independentes (ordinais)

Q de Cochran: k amostras emparelhadas binárias