Objetivo é encontrar a melhor solução possível, onde quantifica a qualidade da solução:

Onde transforma um vetor em um numero real.

Função objetivo:

Direção de otimização, maximizar (solução fornece o maior valore possível) ou minimizar (minimiza o custo), exemplo minimizar o tempo de viagem, ou maximizar o lucro.

Otimizador Global: busca a melhor entre todas as soluções viáveis, onde busca o minimo ou maximo global.

site: https://en.wikipedia.org/wiki/Global_optimization, acesso 03 de setembro 2025.

Otimizador Local: não tão complexo comparado a achar o otimizador global (minimo ou maximo), em muitos casos buscamos o minimo ou maximo local.

Restrições:Condições que limitam as variáveis de decisão, expressas como igualdades ou desigualdades lineares (ex: disponibilidade de ingredientes, demanda máxima ou mínima de um produto). 

Álgebra linear:

Vetores:

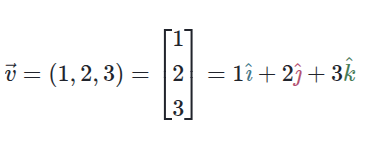
site:https://pt.khanacademy.org/math/multivariable-calculus/thinking-about-multivariable-function/x786f2022:vectors-and-matrices/a/vectors-and-notation-mvc, acesso 2 outubro de 2025.

Matriz: linhas x colunas

site:https://pt.khanacademy.org/math/multivariable-calculus/thinking-about-multivariable-function/x786f2022:vectors-and-matrices/a/matrices–intro-mvc, acesso 2 outubro de 2025.

Produto Vetor x Matrix:

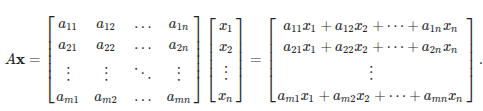
Produto Matriz x Matriz:

Transposta: inverte coluna e linhas.