Discretos

Bernoulli – 1 ou 0 (Ex. sim ou não ou sucesso ou não sucesso):

A probabilidade de X assumir um determinado valor x (0 ou 1) é dada por P(X = x) = p^x(1-p)^1-x

Exemplo:

Um inspetor de qualidade extrai uma amostra aleatória de 10
tubos armazenados num depósito onde, de acordo com os padrões
de produção, se espera um total de 20% de tubos defeituosos.
Qual é a probabilidade de que não mais do que 2 tubos extraídos
sejam defeituosos?
Se X denotar a variável “número de tubos defeituosos em 10
extrações independentes e aleatórias”, qual o seu valor esperado?
Qual a variância?

Note que a variável aleatória X = número de tubos defeituosos em
10 extrações tem distribuição binomial, com parâmetros n = 10 e
p = 0,2. Portanto, “não mais do que dois tubos defeituosos” é o
evento {X ≤ 2}. Sabemos que, para X ∼ b(10 , 0,2)

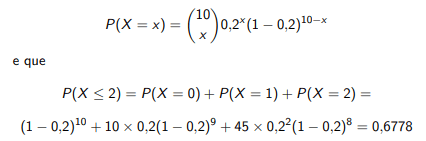
Se X ∼ b(n, p), então
E(X) = np Var(X) = np(1 − p)
Basta então aplicar os valores fornecidos para vermos que o
n´umero esperado de tubos defeituosos num experimento com 10
extrações é de 2, e que a variância é de 1,6.

Binomial:

A distribuição binomial é usada para calcular a probabilidade de obter um certo número de “sucessos” em um número fixo de “tentativas” (ensaios de Bernoulli), onde cada tentativa tem apenas dois resultados possíveis e os resultados são independentes.

Fórmula:

• n: O número total de tentativas.
• k: O número de sucessos desejados.
• p: A probabilidade de sucesso em uma única tentativa.
• q (ou 1-p): A probabilidade de fracasso em uma única tentativa.

Como usar a fórmula:

A fórmula geral da distribuição binomial é: P(X=k) = C(n, k) * p^k * q^(n-k) 

Onde: 

• P(X=k): A probabilidade de obter exatamente k sucessos.
• C(n, k): O coeficiente binomial, que representa o número de combinações de escolher k sucessos em n tentativas.
• p^k: A probabilidade de k sucessos.
• q^(n-k): A probabilidade de (n-k) fracassos.

Poisson:

média e variância valores iguais.

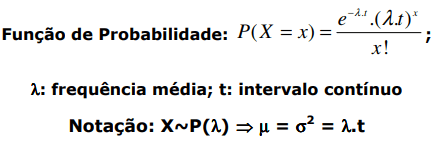
Resumo:

A Distribuição de Bernoulli descreve o resultado de um único ensaio com dois resultados possíveis (sucesso ou fracasso); 

A Distribuição Binomial modela a soma de vários ensaios de Bernoulli independentes, contando o número de sucessos; 

A Distribuição de Poisson lida com a probabilidade de um certo número de eventos ocorrerem num intervalo fixo de tempo ou espaço, sendo útil para eventos raros.

Continuos

Uniforme: é um modelo de probabilidade onde cada resultado possível dentro de um determinado intervalo tem a mesma probabilidade de ocorrer.

Distribuição normal: uma distribuição contínua e simétrica ao redor da média, a maioria dos valores tende a se agrupar ao redor da média e valores que se afastam da média (para mais ou para menos) tendem a ser menos frequentes.

site: https://www.blog.psicometriaonline.com.br/distribuicao-normal/, acesso 16 setembro 2025.

Normal padrão:uma distribuição normal teórica especial, cuja média é 0 e o desvio-padrão é 1.

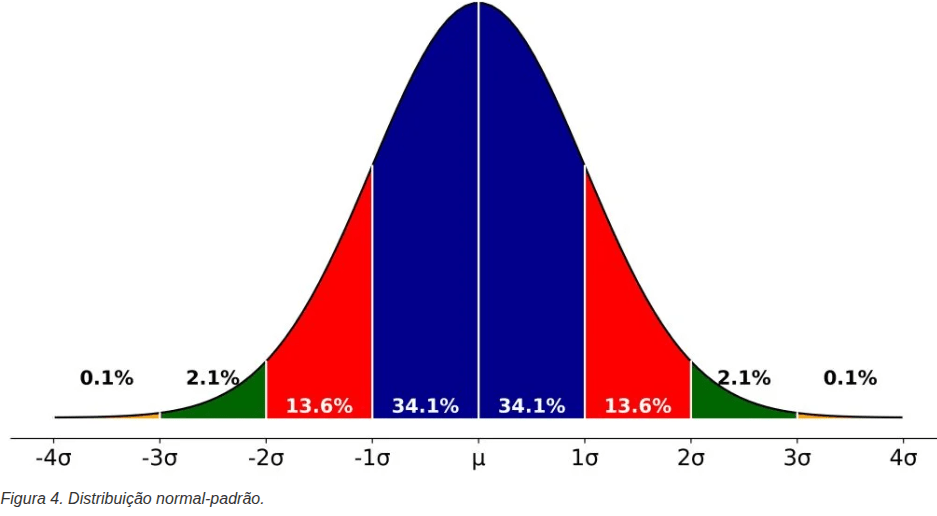
Exponencial:

É uma distribuição de probabilidade contínua que modela o tempo até a ocorrência de um evento em um processo de Poisson, ou seja, eventos que acontecem de forma independente e a uma taxa constante. Ela descreve a probabilidade de um evento ter uma duração ou ocorrer dentro de um certo tempo, sendo muito usada em áreas como análise de confiabilidade (tempo de vida de componentes) e tempos de espera. 

Exemplo: você quer saber a probabilidade de um aparelho eletrônico continuar funcionando após 3 anos, sabendo que, em média, ele dura 2 anos. A probabilidade de ele continuar funcionando diminui com o passar do tempo, o que é uma característica da distribuição exponencial. 

site: https://www.youtube.com/watch?v=87dvB9v1pRI, acesso 16 de setembro de 2025.

t-student

Parecida com a normal , mas com a cauda mais “pesada”, indicando uma maior probabilidade de ocorrerem valores extremos, mas aproxima-se da distribuição normal à medida que o número de graus de liberdade aumenta.

É uma distribuição de probabilidade em forma de sino, semelhante à distribuição normal, mas utilizada quando se trabalha com amostras pequenas ou com a variância populacional desconhecida.

• Amostras pequenas: É a escolha ideal quando o tamanho da amostra é pequeno (geralmente inferior a 30 observações). 
• Variância populacional desconhecida: Utiliza-se quando não se sabe o desvio padrão ou a variância da população. 

Qui-quadrado

é uma distribuição de probabilidade contínua usada em inferência estatística para testes de hipóteses, especialmente para avaliar se os dados observados se ajustam a uma distribuição esperada (teste de aderência) ou para testar a independência entre variáveis categóricas. Caracteriza-se por ser assimétrica à direita e definida por um parâmetro chamado graus de liberdade (k). 

F de Fisher-Snedecor

é uma distribuição de probabilidade de variáveis contínuas, definida como a razão de duas variáveis aleatórias independentes com distribuição qui-quadrado, divididas pelos seus respetivos graus de liberdade. É usada principalmente para inferência sobre a razão entre duas variâncias e em técnicas estatísticas como a Análise de Variância (ANOVA), onde compara a variabilidade entre grupos com a variabilidade dentro dos grupos. 

• Assimetria: É uma distribuição assimétrica à direita, com valores que assumem apenas valores positivos. 
• Graus de Liberdade: É caracterizada por dois parâmetros: os graus de liberdade do numerador e do denominador, que influenciam a forma da distribuição.