Parâmetros, estimadores e distribuição.

• Parâmetro são desconhecidos e queremos estimar.
• Estimador é uma função da amostra, ele é uma variável aleatória que varia com a amostra.
• Distribuição amostrais dos estimadores.

Exemplo:

Suponha que temos uma população com distribuição normal cuja média μ e desvio-padrão σ .

Abaixo vamos ver:

• Viés;
• Consistência;
• Eficiência.

Distribuição amostral média:

É a distribuição de probabilidades de todas as médias amostrais possíveis de um certo tamanho (n) retiradas de uma população .

Exemplo: Se você tirar várias amostras de tamanho 10 de uma população, você obterá várias médias. A distribuição dessas médias é a distribuição amostral da média.

Exercicio:

Definição da População: Considera-se uma urna contendo três bolinhas numeradas de 1, 2 e 3. Esta é a população.

Definição da Amostra: . É retirada uma amostra aleatória com reposição de duas bolinhas da urna.O tamanho da amostra é n=2.

Possíveis Amostras e Suas Médias:

Listagem das Amostras: . Todas as combinações possíveis de duas bolinhas com reposição são listadas.

O espaço amostral 𝑆 é dado por:

S={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}
O número total de amostras possíveis é :

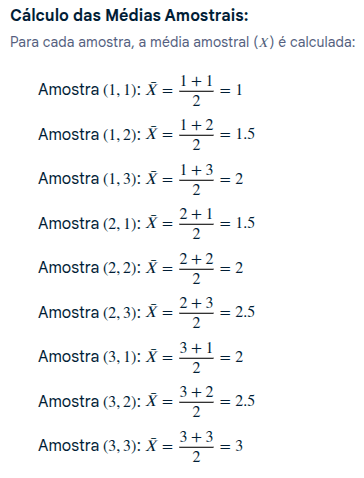
Estimador não viesado:

Um estimador é não enviesado , se em média, não está tedendo a superestimar ou subestimar o verdadeiro valor do parâmetro.

A distribuição amostral da média, ou média amostral (X̄), é a distribuição de todas as médias possíveis de amostras aleatórias de um determinado tamanho (n) extraídas de uma população. Este estimador é não viesado porque o seu valor esperado é igual à média populacional (µ). A distribuição amostral da média, graças ao Teorema do Limite Central, tende a ser aproximadamente normal, mesmo que a população original não seja normal, especialmente para amostras grandes. 

Por que a média amostral (X̄) é um estimador não viesado? 

• Um estimador é não viesado (ou não viciado) se o seu valor esperado é igual ao parâmetro populacional que ele está a tentar estimar. 
• No caso da média, o valor esperado da média amostral é igual à média populacional (E(X̄) = µ). 
• Isso significa que, em média, a média amostral não tende a superestimar ou subestimar a verdadeira média da população. 

Consistência do Estimador:

• Definição: Um estimador é consistente se, ao aumentar o tamanho da amostra (n), o seu valor se aproxima cada vez mais do valor real do parâmetro populacional que ele tenta estimar. 
• Como funciona: Para um estimador da média ser consistente:
  • A esperança (valor esperado) deve tender ao parâmetro: Ou seja, em média, o estimador deve se aproximar do valor real da média populacional, mesmo com a variabilidade natural das amostras. 
  • A variância deve tender a zero: À medida que n aumenta, a dispersão dos valores do estimador deve diminuir, indicando que os valores obtidos com amostras maiores estão mais concentrados em torno do parâmetro populacional.

Em resumo:

Estimador Não Viesado, mas Não Consistente

• Definição: Um estimador não viesado tem o seu valor esperado igual ao verdadeiro parâmetro populacional (E(T) = θ). Um estimador não consistente tem a sua variância que não tende a zero à medida que o tamanho da amostra cresce. 
• Exemplo: Considere a variância de uma população, σ². Um estimador para ela pode ser obtido usando a média de frequência amostral, que é o estimador de variância tendencioso do livro e sua amostra. 

Estimador Viesado, mas Consistente

• Definição: Um estimador viesado tem um viés não nulo, ou seja, o seu valor esperado não é igual ao parâmetro real. Um estimador consistente tem a sua variância que tende a zero à medida que o tamanho da amostra se aproxima do infinito. 
• Exemplo: Um estimador da variância populacional, σ², usando o denominador de n, pode ser usado para a variância da amostra. Este estimador tem um viés, mas é consistente. 

Como Identificar Estimadores Não Viesados e Consistentes

• Um estimador é não viesado se E(T) = θ, e é consistente se a variância de T tende a zero quando o tamanho da amostra n tende ao infinito. 
• Em geral, os estimadores não viesados e consistentes são preferíveis, pois fornecem estimativas mais precisas e não tendem a subestimar ou superestimar o parâmetro ao longo do tempo. 
• Variância Pequena (Eficiência): 
  Um bom estimador deve ser consistente e ter uma variância pequena, significando que a variância do estimador tende a zero quando o tamanho da amostra é grande. 

Eficiência do Estimador:

Variância Pequena (Eficiência): 
Um bom estimador deve ser consistente e ter uma variância pequena, significando que a variância do estimador tende a zero quando o tamanho da amostra é grande. 

Erro quadratico médio (MSE):

Soma da variância do estimador + o viés ao quadrado do estimador, fornecendo uma maneira útil de calcular o MSE e implicando que, no caso de estimadores não tendenciosos, o MSE e a variância são equivalentes. MSE ⁡ ( θ ^ ) = Var θ ⁡ ( θ ^ ) + Bias ⁡ ( θ ^ , θ ) 2.

• O quadrado do vies: o quanto o estimador está longe do valor verdadeiro.
• A variância: o quanto o estimador pode variar em diferentes amostras da população.

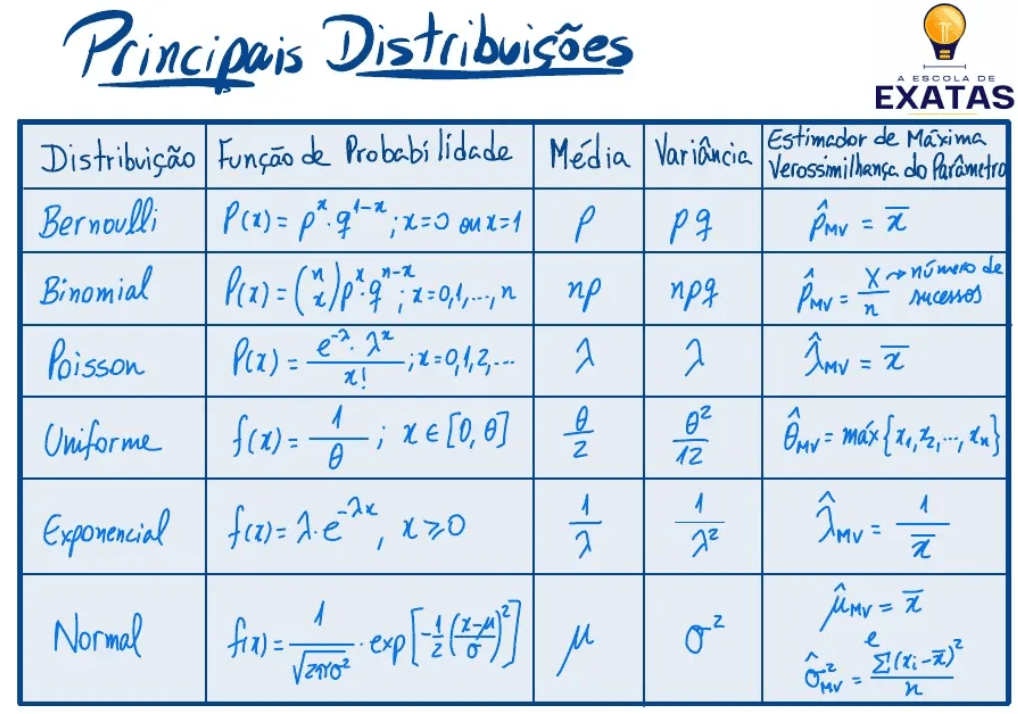
Máxima Verossimilhança (MLE):

A “máxima verossimilhança” (ou Estimativa de Máxima Verossimilhança – MLE) é um método estatístico para estimar os parâmetros de um modelo probabilístico, procurando os valores que tornam os dados observados o mais prováveis possível.

o principio da verossimilhança afirma que devemos escolher aquele valor do parâmetro desconhecido que maximiza a probabilidade de obter a amostra particular observada, ou seja, o valor que torna aquela amostra a “mais provável”. Exemplo de Verossimilhança: A função de verossimilhança para estimar a probabilidade de um pouso de uma moeda sem conhecimento prévio de seu lançamento.

Verossimilhança vs. Probabilidade

“Não confunda verossimilhança com probabilidade. Enquanto a probabilidade mede a chance de observar dados específicos dado um conjunto de parâmetros, a verossimilhança mede a plausibilidade de um conjunto de parâmetros dado os dados observados. Em outras palavras, a verossimilhança é uma função dos parâmetros, enquanto a probabilidade é uma função dos dados. Essa distinção é crucial para a correta aplicação de métodos estatísticos.”

site: https://estatisticafacil.org/glossario/o-que-e-verossimilhanca-entenda-o-conceito/, acesso 25 setembro de 2025.

site: https://pt.scribd.com/document/838190048/Estimadores-de-Ma-xima-Verossimilhanc-a, acesso 25 setembro 2025.

Intervalo de confiança:

“O intervalo de confiança é um intervalo numérico construído ao redor da estimativa de um parâmetro. Ele utiliza um procedimento que, ao ser repetido em várias amostras hipotéticas, gera intervalos contendo o valor verdadeiro do parâmetro em X% dos casos.

Vamos dividir essa definição em partes. Primeiramente, o intervalo de confiança possui limites inferior e superior, calculados ao redor da estimativa de um parâmetro, θ-chapéu.”

Lima, M. (2024, 18 de dezembro). O que é intervalo de confiança? Blog Psicometria Online. https://www.blog.psicometriaonline.com.br/o-que-e-intervalo-de-confianca.

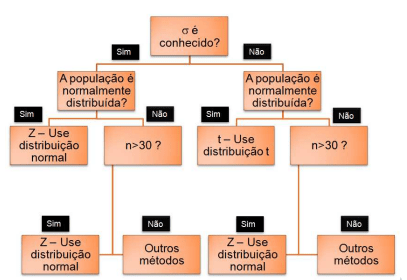
Intervalo de confiança para média com variância conhecida:

Para um intervalo de confiança da média populacional (μ) com variância (σ²) conhecida, utiliza-se a distribuição normal e a fórmula: x̄ ± Z * (σ/√n), onde x̄ é a média amostral, Z é o valor crítico da distribuição normal para o nível de confiança desejado (ex: 1,96 para 95% de confiança), σ é o desvio padrão populacional e n é o tamanho da amostra.

Intervalo de confiança para média com variância desconhecida:

Para construir um intervalo de confiança para a média populacional com variância desconhecida, usa-se a distribuição t de Student em vez da distribuição normal padrão, pois a variância populacional é desconhecida e, geralmente, trabalha-se com amostras pequenas. A fórmula do intervalo é a média amostral mais ou menos o produto do valor t de Student (determinado pelo nível de confiança e graus de liberdade) pela margem de erro, que é o desvio padrão amostral dividido pela raiz quadrada do tamanho da amostra. 

Passos para calcular o intervalo de confiança:

1. Determinar o nível de confiança: Geralmente são 90%, 95% ou 99%.
2. Calcular os graus de liberdade (gl): Em geral, gl = n – 1, onde n é o tamanho da amostra.
3. Encontrar o valor t de Student: Utilize uma tabela t de Student ou software estatístico com base no nível de confiança e nos graus de liberdade.
4. Calcular o desvio padrão amostral (s): Esta é a medida da variabilidade da amostra.
5. Calcular o erro padrão da média: Divida o desvio padrão amostral pela raiz quadrada do tamanho da amostra (n).
6. Calcular a margem de erro: Multiplique o valor t de Student pelo erro padrão da média.
7. Construir o intervalo: Some e subtraia a margem de erro da média amostral (x̄) para obter os limites inferior e superior do intervalo. 

Exemplo prático:
Assumindo que você tem uma amostra de tamanho n, com média x̄ e desvio padrão s, e deseja um intervalo de confiança de 95%: 

• Cálculo:
• x̄ ± t * (s / √n). 

site: https://est.ufmg.br/~marcosop/est031/aulas/Capitulo_8_1.pdf, acesso 25 de setembro de 2025.