Testes de Hipótese – 2

dbasamantalekecinskas Estatística, Sem categoria

Será que nos dados da população as variáveis são relevantes para o modelo ou são mero fruto do acaso?

Parâmetros da população e Estatisticas da amostra.

site: https://www.questionpro.com/blog/pt-br/populacao-e-amostra/, acesso 26 setembro de 2025.

A variância influencia fortemente a significância.

1. Conceito de significância estatística

  • A significância vem de testes de hipótese.
  • Ela mede se um efeito observado (ex.: diferença entre médias, coeficiente de regressão, correlação) é provável de ter ocorrido por acaso ou se é um efeito consistente.
  • É expressa por meio do valor-p: quanto menor o valor-p, maior a evidência contra a hipótese nula (de “não efeito”).

2. Papel da variância

  • A variância dos dados afeta o erro padrão (desvio padrão da média ou do estimador).
  • Quanto maior a variância, maior a dispersão dos dados → maior o erro padrão → o teste estatístico perde poder → é mais difícil encontrar significância.
  • Quanto menor a variância, os dados ficam mais concentrados → menor o erro padrão → aumenta a chance de detectar um efeito como significativo (se ele existir).

Em fórmulas simplificadas, um teste t é:

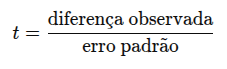
E o erro padrão depende da variância:

Ou seja: se a variância (σ²) é alta, o erro é grande → t cai → p-valor aumenta → menor chance de significância.

O que são dados paramétricos?

São dados que seguem uma distribuição conhecida, geralmente a distribuição Normal (Gaussiana), ou que podem ser transformados para se aproximar dela (por exemplo, usando Box-Cox).

Quando dizemos que uma análise é paramétrica, significa que:

  • Faz suposições sobre os parâmetros da população (média, variância, etc.);
  • Assume que os dados vêm de uma distribuição específica (na maioria das vezes, normal);
  • Usa fórmulas matemáticas que dependem dessas premissas.

🔹 Exemplos de testes paramétricos

  • Teste t de Student (médias)
  • ANOVA (comparação de médias entre grupos)
  • Correlação de Pearson
  • Regressão linear

🔹 Características dos dados paramétricos

  1. Normalidade – os dados seguem (ou aproximadamente seguem) distribuição normal.
  2. Homocedasticidade – variâncias dos grupos comparados são iguais ou semelhantes.
  3. Independência – as observações não podem estar correlacionadas indevidamente.
  4. Escala intervalar ou de razão – precisam ser dados numéricos contínuos (ex.: altura, tempo, tamanho de banco de dados em GB).

🔹 Comparação com dados não paramétricos

  • Paramétricos: mais poderosos, mas exigem que os pressupostos sejam atendidos.
  • Não paramétricos: usados quando os dados não seguem normalidade ou não têm variâncias iguais (ex.: teste de Mann-Whitney, teste de Kruskal-Wallis).

Testes de Hipótese para dados Paramétricos (pressupõem normalidade dos dados):

OBS: para utilizar testes paramétricos , antes deve realizar teste de normalidade !!! (Ex. Shapiro-wilk-amostras pequenas < 30)

  • Teste para a média (com variância conhecida)
  • Teste para a média (com variância desconhecida)
  • Teste para a variância
  • Teste t pareado (comparação de médias em duas amostras dependentes)
  • Teste t independente (comparação de médias em duas amostras independentes)
  • ANOVA (comparação de médias em três ou mais grupos independentes)
  • Teste para comparação de variâncias

No quadro de decisão em testes de hipótese em formato de imagem, com destaque visual:

  • Erro Tipo I (α) em vermelho claro → rejeitar H₀ quando ela é verdadeira.
  • Erro Tipo II (β) em amarelo claro → não rejeitar H₀ quando ela é falsa.
  • As demais situações mostram as decisões corretas.

🚀 Passos para Realizar um Teste de Hipóteses

  1. Definir a variável em estudo
    • Identificar qual parâmetro será avaliado (média, variância, proporção etc.).
  2. Definir as hipóteses
    • Hipótese nula (H₀): não há efeito/diferença (hipótese padrão).
    • Hipótese alternativa (H₁): existe efeito/diferença.
  3. Escolher o nível de significância (α)
    • Probabilidade de cometer Erro Tipo I.
    • Valor comum: α = 0,05 (5%).
  4. Selecionar o teste estatístico
    • Depende do tipo de dado e do problema:
      • Teste z → variância conhecida e amostra grande.
      • Teste t → variância desconhecida ou amostra pequena.
      • ANOVA, Qui-quadrado, F de Snedecor, etc.
  5. Calcular a estatística de teste
    • Usar a fórmula do teste escolhido.
    • Comparar com valores críticos ou p-valor.

🧪 Testes de Hipótese para a Média Populacional:

Distribuição usada:

  • Se σ (variância populacional) é desconhecida → teste t de Student (mais comum).
  • Se σ é conhecida → pode-se usar o teste Z.

Para verificar se a média populacional μ é igual a um valor específico μ0​:

🔹 Teste bicaudal (duas caudas)

  • H₀: μ=μ0
  • H₁: μ≠μ0
    👉 Usado quando queremos detectar qualquer diferença (maior ou menor).

🔹 Teste unicaudal superior (uma cauda à direita)

  • H₀: μ=μ0
  • H₁: μ>μ0
    👉 Usado quando queremos verificar se a média é maior que μ0​.

🔹 Teste unicaudal inferior (uma cauda à esquerda)

  • H₀: μ=μ0
  • H₁: μ<μ0
    👉 Usado quando queremos verificar se a média é menor que μ0.

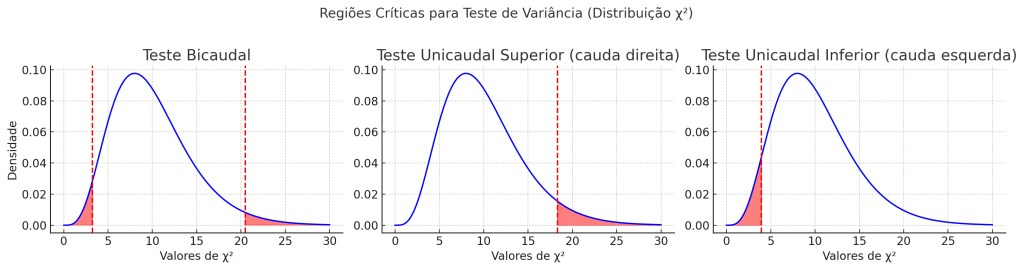
🧪 Teste para a Variância Populacional (qui-quadrado):

Ele é a versão análoga ao que vimos para a média, mas aqui usamos como estatística de teste a qui-quadrado .

Distribuição usada:

  • Porem assumimos que a média é conhecida e a variância que é desconhecida.

Seguem os gráficos das regiões críticas para o teste de variância usando a distribuição qui-quadrado:

Teste unicaudal inferior → rejeita H0 se χ2 cair na cauda esquerda.

Teste bicaudal → rejeita H0 se χ2 cair nas extremidades (caudas vermelhas).

Teste unicaudal superior → rejeita H0 se χ2 cair na cauda direita.

Resumo:

Deixe um comentário