Otimização Linear:

Otimização Linear, ou Programação Linear (PL), é um método matemático para tomar a melhor decisão em um problema, maximizando ou minimizando um objetivo (como lucro ou custo) sujeito a um conjunto de restrições representadas por equações lineares. Ela é aplicada na pesquisa operacional para resolver situações complexas do mundo real, como planejamento de produção, definindo as quantidades ideais de produtos a fabricar para otimizar o lucro, ou criando misturas com o menor custo possível, respeitando a disponibilidade de componentes. 

Função Objetivo é linear: min ou max da função linear abaixo.

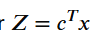
Restrições tambem linear:  Limitações de recursos (materiais, tempo, mão de obra), expressas como inequações ($$<= ou >=) ou equações ($$=) lineares.

s.a.: Ax >= b x>=0

Objetivo: Maximizar o lucro ou minimizar custos, expresso como uma função linear $$.

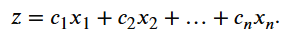
Elementos Principais:

• Função Objetivo:Uma função matemática (linear) que expressa o objetivo do problema, como maximizar o lucro ou minimizar o custo. 
• Variáveis de Decisão:As variáveis que precisam ser determinadas para atingir o objetivo (ex: quantidade de cada produto a ser produzida). 
• Restrições:Condições que limitam as variáveis de decisão, expressas como igualdades ou desigualdades lineares (ex: disponibilidade de ingredientes, demanda máxima ou mínima de um produto). 

Objetivos exemplos:

1. Ter unico otimizador global.
2. Ter infinitos otimizadores globais
3. Ser infactivel.
4. Ser factivel, mas sem otimizador.

• em python podemos utilizar as bibliotecas linprog, mip, pub

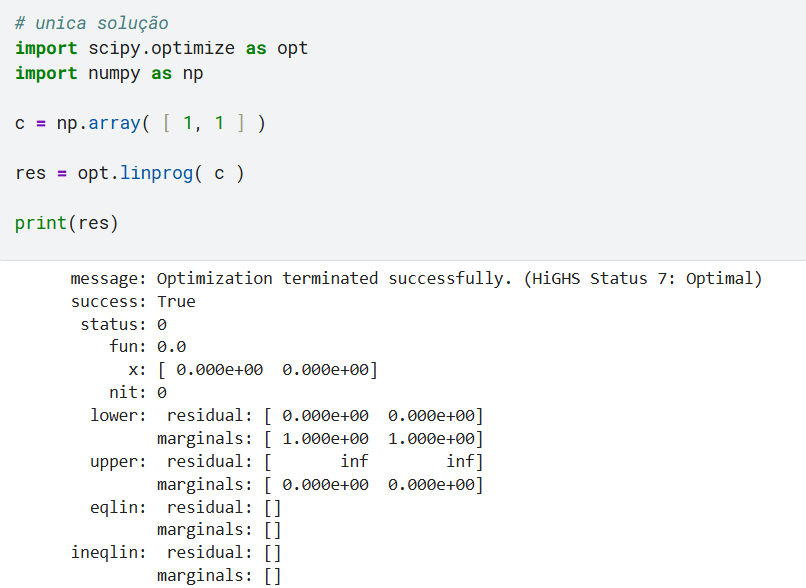
1) Unica solução:

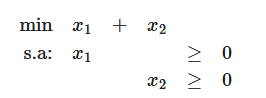
Obs: por padrao no linprog bounds = ( 0, None ), que são as restrições da “Unica solução”

2) Infinitas soluções:

Obs.: Aqui as restrições acima estão em A_eq e b_eq

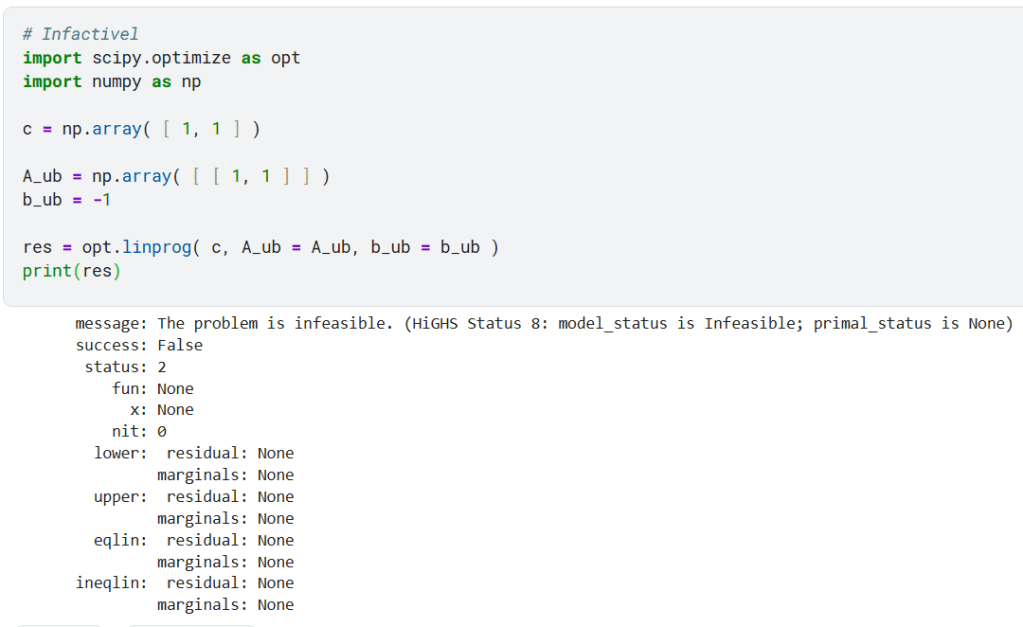
3) Infactivel

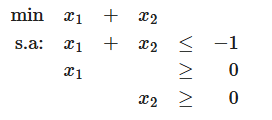
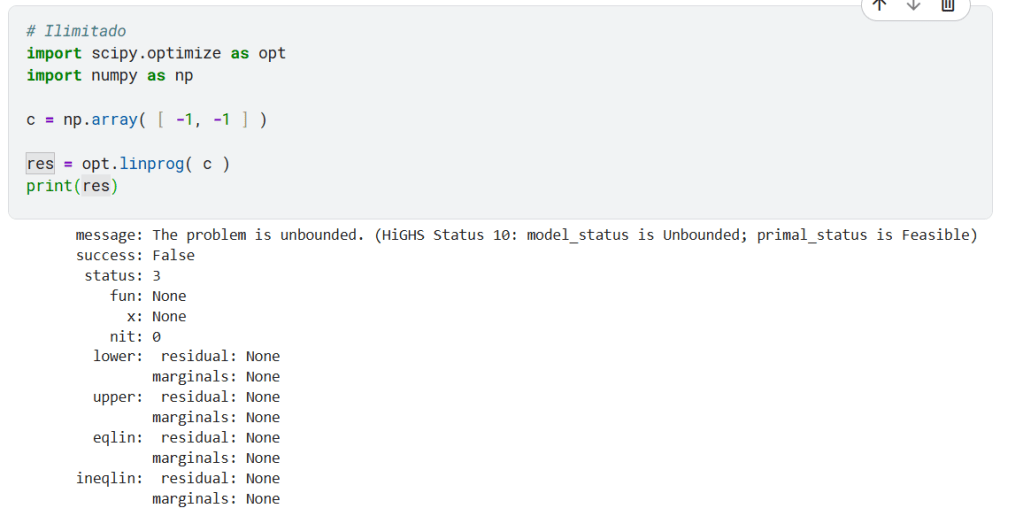
4) Ilimitado

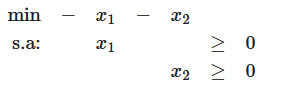
Alguns Exemplo de otimizador em python:

com a biblioteca do scipy.optimize.minimize_scalar extraimos o minimo e no código abaixo adicionamos um intervalo de limite para ele achar o minímo.

Restrições:

Exemplos de Otimização Linear: